散列存储结构

ou99孽缘

在介绍这种存储结构之前先扫扫盲，下图很直观的介绍了数据结构的分类。


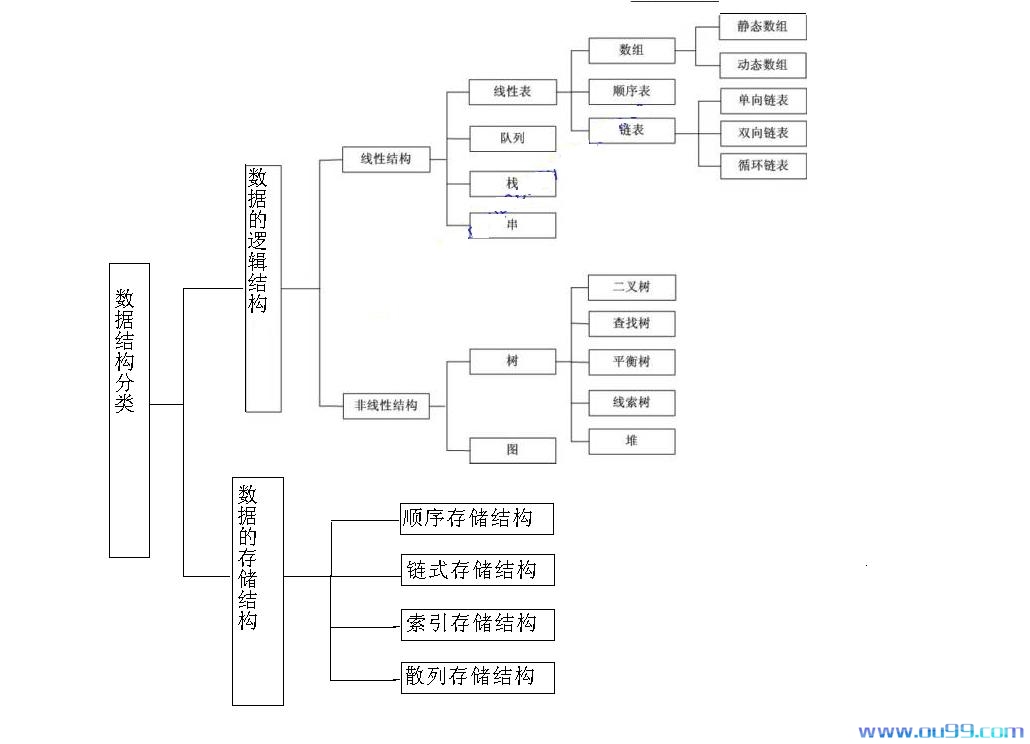
在这里要分清逻辑结构与存储结构的区别。逻辑结构值数据间的逻辑关系，存储结构是数据的物理关系。
数据结构的重要性是不容忽视的，数据结构+算法=程序。可见数据结构的重要性是与算法相同的。如果说算法是程序的灵魂，那数据结构就是程序的实体。
这里就先介绍散列存储结构。这种存储方法是在数据元素与其存储器上的存储位置之间建立一个映象关系。根据这个映象关系，已知某数据元素
就可以知道他的存储地址。这种存储结构的关键是设计这个映射函数。
哈希表的建立
以线性表中的每个元素的关键字Kewing自变量，通过一种函数H(K)算出函数值，然后将该元素存入H(K)所指定的响应的存储单元。
对于某个哈希函数H(K)和两个关键字K1和K2，如果K1不等于K2，H(K1)=H(K2)，这种现象称为冲突。在构造哈希函数时应避免冲突，但没有冲突的函数是不好找的，因为通常哈希函数ushi一个压缩映象，即关键字集合打，地址集合小。由于哈希法用哈希函数转换记录关键字得到存储地址，吧个记录散列到响应的存储单元里去，所以也称之为散列地址法或关键字转换法。对于哈希法，主要考虑两个问题：
1) 构造一个合适的哈希函数。分析数据元素的关键字集合值特点，找出适当的函数。
2) 如何解决冲突。哈希函数应具有就好的散列性，冲突时不可避免的，但应尽量减少。处理冲突的方法如下：
处理冲突——假设哈希表的地址集为0~n-1,冲突是指由关键字得到的哈希 地址为j(0<=j<=n-1)的位置上已存有记录,则“处理冲突”就是为该关键字的记录找到另一个“空”的哈希地址. 在处理冲突过程中可能得到一个地址序列Hi (i=1,2,…,k),即在处理哈希地址的冲突时,若得到的另一个哈希地址H1仍然发生冲突,则再求下一个地址 H2,若H2仍然冲突,再求得H3.依次类推,直到Hk不发生冲突为止,则Hk为记录在表中的地址.
常用的处理冲突的方法：(1)开放定址法。(2)链地址法。(3)再哈希法。(4)公共溢出区法
(1)开放定址法。
Hi=(H(key)+di) MOD m i=1,2,...,k(k<=m-1)
其中m为表长，di为增量序列
di有三种取法:
(1)di=1,2,3,...m-1，称线性探测再散列。
(2)di=1平方，-1平方，2平方，-2平方···，K平方，-K平方 （K<=m/2）称二次探测再散列.
(3)di=伪随机数序列,称伪随机探测再散列.
例:有关键字序列(17,60,29,38…)
哈希函数为:H(key)=key mod 11,表长为11 哈希表为:



解决冲突:用开放定址法 Hi=(H(key)+di) MOD m
(1)线性探测再散列 di=1,2,3,...m-1
H1=(H(38)+1) mod 11 =(5+1) mod 11=6
H2=(H(38)+2) mod 11 =(5+2) mod 11=7
H3=(H(38)+3) mod 11 =(5+3) mod 11=8
关键字38的哈希地址为8
(2) 二次探测再散列
H1=(H(38)+1) mod 11 =(5+1) mod 11=6
H2=(H(38)-1) mod 11 =(5-1) mod 11=4
关键字38的哈希地址为4
3)伪随机探测再散列 di=9,1,6,4…
H1=(H(38)+9) mod 11 =(5+9) mod 11=3
关键字38的哈希地址为3
(2)链地址法
将所有关键字为同义词的记录存储在同一线性链表中。
假设某哈希函数产生的哈希地址在区间在[0,m-1]上,则设立一个指针数组:
chainhash: array [0..m-1] of pointer;
其每个分量的初值为NILL.凡哈希地址为i的记录都插入到chainhash的链表中.
例:有关键字序列(19,14,23,01,68,20,84,27,55,11,10,79)
哈希函数:H(key)=key mod 13


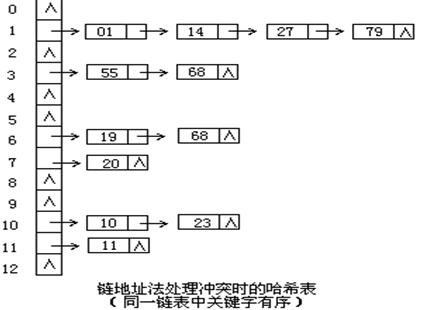
(3)再哈希法
Hi=RHi(key) i=1,2,3,…,k当发生冲突时，使用第二个、第三个、哈希函数计算地址，直到无冲突
为止。 缺点：计算时间增加。
(4)公共溢出区法
建立一个公共溢出区 假设哈希函数的值域为[0,m-1],则设向量hashtable[0..m-1]为基本表，每个
分量存放一个记录,另外设立存储空间向量overtable[0..v]为溢出表,用以存储发生冲突的记录。
例:有关键字序列(19,14,23,01,68,20,84,27,55,11,10,79)
哈希函数:H(key)=key mod 13
解决冲突方法:建立一个公共溢出区
在哈希表上查找的过程和构造哈希表的过程基本一致。
下载 (17.12 KB)
2010-8-14 22:18